Cahit Kayra’dan Marjinal Şiir Teorileri

Şiir incelemelerinde nesnel teoriler uygulanabilir mi?

1917 yılında İstanbul’da doğan Cahit Kayra geçtiğimiz aylarda 101. yaş gününü kutladı. Koca çınarı ekonomi ve maliye alanlarında verdiği emekten tanıyoruz. Kırktan fazla eserinde mesleki araştırmaların yanı sıra çeviri, anı, öykü ve romanları da bulunmaktadır. 2016 yılında Marjinal Şiir Teorileri adlı kitabı Tarihçi Kitabevi’nden yayımlandı. Şiir eleştirisinde nesnel açıdan öncü bir çalışma. Bu kitabı şiir severlerin ve tahlil edenlerin dikkatine çekmek istiyorum, sizlere kitabı tanıtırken artı ve eksi yanlarını göstermeyi ve gelişim alanlarını açıklamayı deneyeceğim. Fakat bunu yapmadan önce matematik ile sanat ilişkisini yeniden hatırlamak sanırım konuyu anlatmak açısından kolaylaştırıcı bir giriş olacak.

Matematik ve Sanat

Sanat bilimi nasıl kullandı? Simetri ve asimetri, uyum, oran gibi kavramların ne anlama geldiğini seziyoruz aslında. Oran ve simetri her koşulda ölçülebilir, sayısal olarak ifade edilebilir veya sezilebilir; sanat da ölçülebilir. Matematik pozitif bilimlerin abecesidir ve günümüzde sanatta tasarım sürecinde başvurulan temel bilgi aynı zamanda. Matematik ve sanatın ilgisini inceleyen yayınlarda genellikle Rönesans döneminden hareketle altın oran, Öklid geometrisi, fraktallar ve müzik konularının ele alındığını görmekteyiz. Rönesans sanatçıları altın oranı tablolarında ve heykellerinde denge ve güzelliği elde etmek amacıyla sıklıkla kullanmışlar. Luca Pacidi’ nin 1509 da yazdığı ve Leonarda da Vinci’ nin resimlerini çizdiği Kutsal Oranlar Hakkında (De Divina Proportione) adlı matematik kitabı altın oran kullanımı anlatır. Daha da eski belgelerde, İÖ. 4 yy. da yaşamış heykeltıraş Polykleitos, Kanon (Canon) adını verdiği ölçüm sisteminde ideal bir erkek bedeni 1:√2 oranıyla tanımlamış. Bir sanatçının yaptığı resim, heykel, şiir, ezgi aslında doğada var olan şeylerin birer taklidi değil midir? Örneğin fasulye bitkisinin bir çubuğa tırmanırken aldığı şekil Helis eğrisidir ve tırmanma süresinin en az olduğu yoldur ve arının bal peteği düzgün altıgendir; daha nice örnekler verebiliriz. Aslında insanın olduğu her yerde matematik yaşam buluyor. İnsanı ilgilendiren her şey matematiği de ilgilendiriyor: Aşk, uzay, sanat, müzik, resim, din… Felsefe ve matematiğin günümüz uygulamalarındaki en güzel sonuçlarından birisi sanattır diyenler haksız olmamalı. Eski çağlardan günümüze kadar sanat ve matematiğin etle tırnak olduğunu görülüyor. Hatta çok da uzağa gitmeyelim, evimizde bizimle matematiğin diliyle konuşan Türk kilimleri serili değil mi?

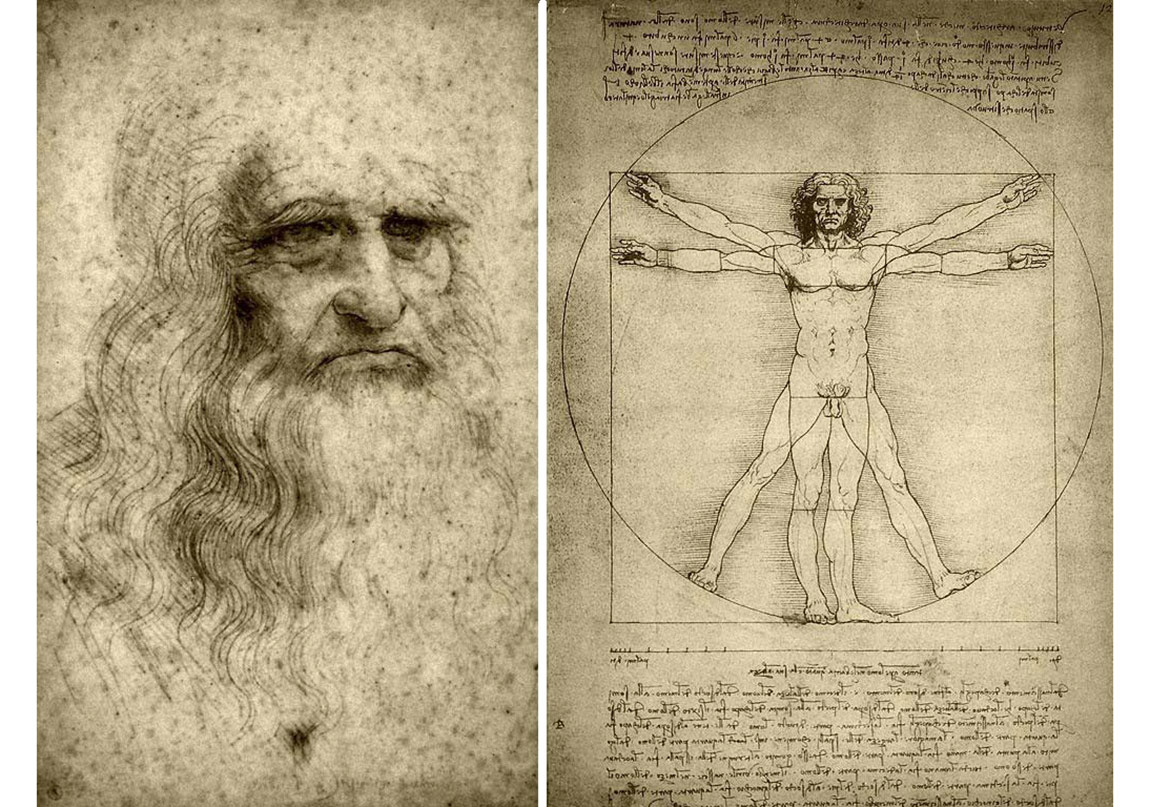
İtalyan ressam Piero della Francesca perspektifi Öklid geometrisinden almış ve uygulamış, buna dair bir de Resimde Perspektif (De Prospectiva Pingendi) adlı bir tez yazmıştır. Leonardo da Vinci sanatı lineer/doğrusal bakış açısıyla yorumlamış, resim ve matematiği sentezleyebilmiştir: Mona Lisa, Son Akşam Yemeği, Müneccim Kralların Tapınması, Meryem’e Müjde gibi tablolarında altın oran vardır. Son Akşam Yemeği adlı tablosuna baktığımızda İsa'nın ve havarilerin oturduğu masanın boyutlarından, arkadaki duvar ve pencerelere kadar altın oranı uygulamıştır.

Doğadaki ve insan üzerindeki, teknolojideki inanılmaz tesadüfler bu sayıyı neredeyse kutsal hale getirmiştir. Antik çağda ressam ve heykeltıraşlar ideal insan ölçüsünün boy uzunluğunun göbekten ayakuçlarına olan uzunluğa oranı, göbekten ayakuçlarına olan uzunluğun göbekten başucuna olan uzunluğa olan orana eşitliği olarak tanımlamışlar. Aynı denklemi parmak boğumları, kol, yüz hatları gibi insanın tüm organlarında da uygulayabiliriz. Bitki yapraklarında, salyangozun kabuğunda çam kozalaklarında, tohumlarda görebilmekteyiz bu oranı.

Sanat ve mimaride ise altın oranı kullanan ve önemli eserlere imza atanların başında Firavun Coser için yapılmış olan Piramit’in 3:1 eğimle ya da 72 derece açı ile üst üste yığılan 6 mastabadan oluştuğu görülmektedir. Bu üçgen altın üçgendir tıpkı Athena’ ya ait Pantheon Tapınağı gibi. Koca Sinan’ın Selimiye’de diktiği kubbe 13 bilinmeyenli bir denklemin cevabıdır. Süleymaniye Camii, İnce Minareli Medrese, Divriği Külliyesi geçmişe dair fen ve matematik bilgisi ile üretilmiş şaheserlerdir.

Matematiksel Sanat

Mathart “matematiksel sanat” denilen kavramı matematiğin yaptığı ve sadece matematik tarafından yapılan sanat olarak tanımlarız. Çevremizde gördüğümüz harika renk uyumları veya gözümüzü alamadığımız o spiraller matematiksel sanatın birer ürünüdür. Metamorfozlar, fraktal geometrisi, sonsuzluk, düzlem, paradokslar matematiğin sanat için ihtiyaç duyduğu aletlerdir. Öklid geometrisi soyuttur aslında çünkü etrafımıza baktığımızda tam küre şeklinde bir ayva ya da tam dik bir üçgen dağ göremeyiz. Fraktal geometrisinde ise nesneleri ne kadar büyütürseniz büyütün ya da ne kadar küçültürseniz küçültün her bir parçası bütünü ile aynı özelliklere sahiptir. Fraktallar daha somut kavramlardan oluştuğundan her insana çekici gelen bir oluşum özelliği taşımaktadır, mesela kabuklu deniz canlılarının karmaşık biçimleri, ağaçların veya damarların dallanmaları, yeryüzü şekilleri fraktalların esinlendikleri doğallıklardan bazıları olarak eserlere konu olabiliyor.

Günümüzde matematiksel sanatçılardan matematikçi Fomenko, bize matematik dünyasından anlar taşırırken daha çok matematikteki çalışma alanı olan topolojik nesneleri ve doğası kolay anlaşılmayan bu dünyayı, olayları resmeder ve mekânlar alabildiğine büyük, insanlar alabildiğine küçük görünür.

Kenneth Snelson’un “tensegrity” adını verdiği modern heykelleri fizikteki vektörel kuvvetler bilgisi ile üretilmiş. Yerçekimine meydan okuyan bir tasarımla dört borudan üçü uçlarından yere çapraz durumda dayanıyor (askerlerin istirahatteyken tüfek çatması gibi) ama dördüncü boru havada, üstelik yere dayalı olanların hepsinden daha da yukarıda ve tuhaf olanı onları birbirine tutturan malzemenin çelik halat olması. Üsteki boruyu alttaki borular ve yerçekimi kendine çekmeye çalışıyor fakat çekim kuvvetinin vektörel toplamı sıfır ettiği için boru yukarıda kalıyor.

Modern zamanların grafik sanatçısı M.C. Escher, matematikçi H.S.M. Coxeter’ in yardımıyla hiperbolik geometriyi sıkça kullanır. Düzlemi düzenli olarak bölerek yaptığı resimlerinde bir ya da birkaç motifi hiçbiri birbirinin üstüne gelmeyecek ve aralarında boşluk kalmayacak şekilde birbirlerini nasıl çevreleyebileceklerini araştırır. Escher bu işlemi çeşitli hayvan figürleri kullanarak fantastik bir şekilde icra eder. Metamorfozlar ile yüzey figür ilişkisi çarpıcı şekilde vurgulanırken, imkânsız olan boyutlar arası yolculuk da resmedilir. Düzlemdeki düzenliliği bozmadan sürekli deforme edilen şekiller birbirine dönüşür, gece gündüze, balıklar kuşa evrilir. Escher'in en vurucu işlerinde paradoks ve sonsuzluk kavramları resmedilmiştir. İmkânsız figürleri kullanarak inşa ettiği dünyalar bizi çelişkiye götürür ve oldukça karmaşık ve detaycı işçiliğiyle matematiğin örgüsüyle çakışır.

Mimariden de bir örnek verirsek, Shawn Brixey’in “Aurora” adını verdiği bir tasarımında ısıya ve basınca duyarlı kristaller bir binanın üzerine sabit olarak yerleştirilmiş ve geceleri büyüyen kristaller, bulunan insanlara ve ısıya göre renkleri ve büyüklüklerini değiştirebiliyor.

Marjinal Şiir Teorileri

Yukarıda sanat eserinin fen ve matematiğe göre en iyi estetiği içerecek şekilde nasıl yaratıldığına dair mimari, resim ve heykelden örnekler vermeye çalıştım. Cahit Kayra’nın Marjinal Şiir Teorileri adlı eserini şimdi size daha iyi anlatabileceğime inanıyorum.

Gelelim konumuza, Cahit Kayra, şiir eleştirisinde edebiyat teorilerinin haricinde bir yöntem öneriyor bize. Şiire bir ölçüm birimi vermek: Şirbil. Dolayısıyla şiirimizi tasarlarken, eleştirirken somut bir ölçüt kullanıyoruz. Şiir incelemelerinde ve eleştirilerinde öznel veya edebiyat/eleştiri teorilerine göre çeşitli çalışmalar mevcut ve yazar bu çalışmaların haricinde onların görmediğini yakaladığını iddia ederken “Sizin şiiriniz kaç şirbil?” diye soruyor. Soru aslında basit; benzetme yaparsak bugün hava sıcak mı sorusuna evet/hayır yerine 23 °C dememizi öneriyor. Diğer bir ifade ile sözcükler, uyak, biçem, ölçek, tema, ahenk, şiir dili, felsefe vb. kavramları değerlendirme konularını kullanan bir ölçütle baş başayız. Buna metrik sistem diyor ve birim olarak şirbil terimini türetmiş. Yani bir şiiri değerlendirirken ona “Bu şiir 5 şirbil ya da 50 şirbil değerindedir.” diyeceksiniz diyor. Kanımca metrik sistem ile güzellikten estetiğe geçiş sağlanıyor ve şiirin estetik boyutu da derecelendirilmiş oluyor. Tıpkı yukarıda örnekler ile göstermeye çalıştığım eserler gibi şiirde altın orana ulaşabileceğimiz bir ölçüt: Şirbil.

Cahit Kayra, metrik sistemi için değerlendirmeye konu olacak tüm faktörlere/parametrelere göre bir matris hazırlamış. Her bir faktöre bir puan aralığı vermiş, örnek olarak ahenk 0-50%, bütünlük 0-65%, özgünlük 0-100%, vb. Soyut bir kavram olan şirbil artı ve eksi değerlerde olabiliyor, bu şekilde şiirdeki düzeni bir denklem ile açıklamaya çalışıyor. Bunun için bize önerdiği formül: Şirbil = Genel Değerler (A) x Özel Değerler (M). Genel değerleri ahenk (A) olarak ele alıyor ve gerçek şiirde en büyük çarpan olarak tanımlıyor. Özel değerleri ise anlam değişkenleri olarak niteliyor; bunlar sevgi, hasret, seks, epik, ontolojik, vb. Şiirin bu ahenk ve anlam ekseni üzerinde nasıl yerleştiği şiirin kaç şirbil olacağı değerini veriyor. Formülde ahengi ana çarpan yapmış, ona göre şiirde ahenk konusu için alaturka makamlar veya çok sesli müzik türlerinden faydalanılabilir. Şirbil formülünde ayrıca diğer değerler adı altında toplama dâhil olan soyluluk, korku, inanç, zekâ, vb. değişkenler de var. Bunların şirbil çarpımına toplam olarak katılması ile daha doğru bir değerlendirme yapılacağını öneriyor. Şirbilin nihai formülünü şöyle yazabiliriz: Ş = (A x M) + ∑ diğer değişkenler.

Cahit Kayra şirbil formülünde ahenk ve anlam dışında tanımladığı değişkenleri çeşitli şiirleri çözümlerken açıklıyor ve değerlerini de veriyor. Bu değişkenler: Özgünlük (0-100%), disiplin (0-25%), bütünlük (0-65%), şekilcilik, postmodern, birikim, zekâ, inanç, felsefe, aşk ve sevgili, korku, hüzün, görkem, asalet, çirkinlik, cinsellik, öfke, taşlama, trajedi olarak tanımlanmış ve her birinin ederi % cinsinden verilmiş. Tabii ki değerlendirmeleri yapmak bu faktörleri kişisel olarak puanlayarak formüle koymak kadar kolay olmasa gerek. Değerlendirmeye aldığı şiirleri kendi yazdığı ürünler, onları incelemiş ve şirbil öğretme aracı olarak kullanmış ve öznel eleştirilerini verirken çeşitli poetik görüşlerini de öğrenme şansımız oluyor.

Cahit Kayra kitabının geliştirmeye açık olduğunu okurlarına açıklıyor. Kitabı okuduktan sonra bazı gelişim alanlarını not aldım defterime ve bazı soruları da. Bunların cevaplarını vermek çok zor olabilir. Belki de şairler, akademisyenler, talebeler bir araya gelmeli ve bu sorunlara bir ortak karar verebilirler:

1. Aynı şirbil puanına sahip şiirlerden hangisi daha iyidir? Diğerinin ahengi, birinin x faktörü fazla ise ve şirbil notları eşitse bu şiirler eşdeğer midir?
2. Teoride gelişime açık olan kısım şirbil puanlarının ne anlama geldiği, örneğin 20 °C bize bir şeyi hissettirir biliriz fakat 12 şirbil ne hissettirir? Şirbil için nasıl bir taksimat yapılmalı?
3. Şirbil hesabını yapabilmek için iyi bir şiir okuru hatta eleştirmeni olmamızı gerektiren faktörlere öznel olarak puan verebilmemiz ve değerlendirebilmemiz için değerli bir birikime ihtiyaç duyabiliriz. Bu durumda olmak pek de kolay değil, şiire yeni başlayanlar için veya şiir severlerin işini kolaylaştıracak puanlama sistemi de geliştirilebilir. Örneğin disiplin faktörü için önerilen şirbil puanı 0-25’tir, bu aralığı kendi içinde zayıf, orta, iyi gibi üç ayrı değerde önerilmesi değerlendirmeyi daha nesnel yapabilir, aksi halde öznel değerlendirmeler ile verilen puanlamalar ile somut değerler birçok eleştirmen de farklı puan toplamına neden olacak ve şiirin şirbil notu sübjektif kalarak, objektif veya evrensel olmayacaktır.
4. Şirbilin en büyük çarpanı ahenk fakat çağdaş şiirde ahenk müzik unsurları ile pek sağlanmıyor, bestelenebilen şiir sayısı oldukça az. Çağdaş şiir için ahenk konusu farklı ele alınmalı ve ona uygun bir formül tasarlanmalı. Varsayılan bir sabiti olmalı ahengin; aksi halde gelenekçi ve yeni şiirin kıyaslanmasında gelenekçi şiir her zaman güçlü olacaktır çünkü ahengin olmadığı bir şiirde A x M değeri M ne olursa olsun sıfır olacaktır ve şirbil sadece özel durumlara bağlı alacağı değerlerin toplamı olacaktır.
5. Şirbil formülünde imge için ayrı bir değerlendirme olmalı mıydı diye sorabiliriz kendimize ki ben olmasını tercih ederdim. Hatta imgeyi tıpkı ahenk gibi çarpan da yapabilirdim. Belki Cahit Kayra imgenin değerini anlam çarpanı içine dâhil etmiş olabilir fakat yine de ayrı ele alınmalı kanısındayım.
6. Ş = (A x M) + ∑ diğer değişkenler formülünün daha iyi bir türevi olabilir. Yazarın çarpan kullanmasının sebebi kitaba göre analitik geometriden faydalanarak şirbil ederlerinin grafik halinde gösterimi olabilir. Daha basit bir yaklaşımla, grafiğe ihtiyaç duymadan ahenk ve anlam dâhil tüm faktörler toplam olarak ya da çarpım olarak elde edilebilir, sanırım bu daha basit bir yorumlama olacaktır. Alternatifler mutlaka türetilebilir, yine bir öneri verecek olursam öznel çözümlemeler için de iyi, orta, kötü şiir için şirbil oranları ilave edilebilir. Bir başka bakış açısı ile de çarpılabilen ve toplanabilen faktörleri ayrı ele alıp sonuçlarını toplamak da şirbil denklemi olabilir, şöyle yazabiliriz: Ş = ∑faktörler + ∏faktörler.
7. Faktörlere verilen puan dilimleri ya da yüzdeler yazarın kendi tecrübelerinden hareketle verilmiş. Örneğin zekâ faktörü için en çok 10% veriyor ve fazla zekânın şiiri öldüreceğini de örneklemeye çalışıyor. Günümüzde bilimsel şiir akımını da düşünürsek bu önermenin geçerli olması zor gözüküyor. Diğer taraftan bu faktörlerin belki de edebiyat fakültelerinde bir anket ile bir tez ile yüzlerce şiir sever tarafından değerlendirilmesi ne kadar iyi olurdu. Belki de bir yüksek lisans talebesi bu işi yapmak ister. Bu sayede bir ortak anlayışa da ulaşmış olurduk.

Son söz olarak, Cahit Kayra’yı Marjinal Şiir Teorileri adlı aykırı ve orijinal çalışmasından dolayı kutlar ve bu konunun geliştirilebilir bir alan olarak bize sunmasından dolayı teşekkür ederim.

Dipnot:

Altın oranı: Bir doğru parçasının |AB| altın orana uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın |AC| büyük parçaya |CB| oranı, büyük parçanın |CB| bütün doğruya |AB| oranına eşit olur. Altın oran, irrasyonel sayıdır ve ondalık sistemde yazılışı 1,618033988749894...'tür.

Topoloji: Esnek madde geometrisi olarak tanımlanabilir. Yırtmadan ve kesmeden, ezip büzerek veya çekip genişleterek yapılan bu dönüşümü bir fonksiyon olarak düşünülebilir ve buna da homeomorfizm denir. Bir karenin daireye, küpün piramide, bir torusun kahve fincanına, daha da ilginci bir noktası atılmış bir kürenin reel düzleme homeomorfik olması gibi.